Difference In Rotation Not Showing Properly in Object Manager?
-
Not quite python related
But I'm trying to understand why Rotation have different representation in object manager to better manipulate it, (despite having the same rotation order)Attached also is the illustration scene.
weird_joint_rotation_difference.c4d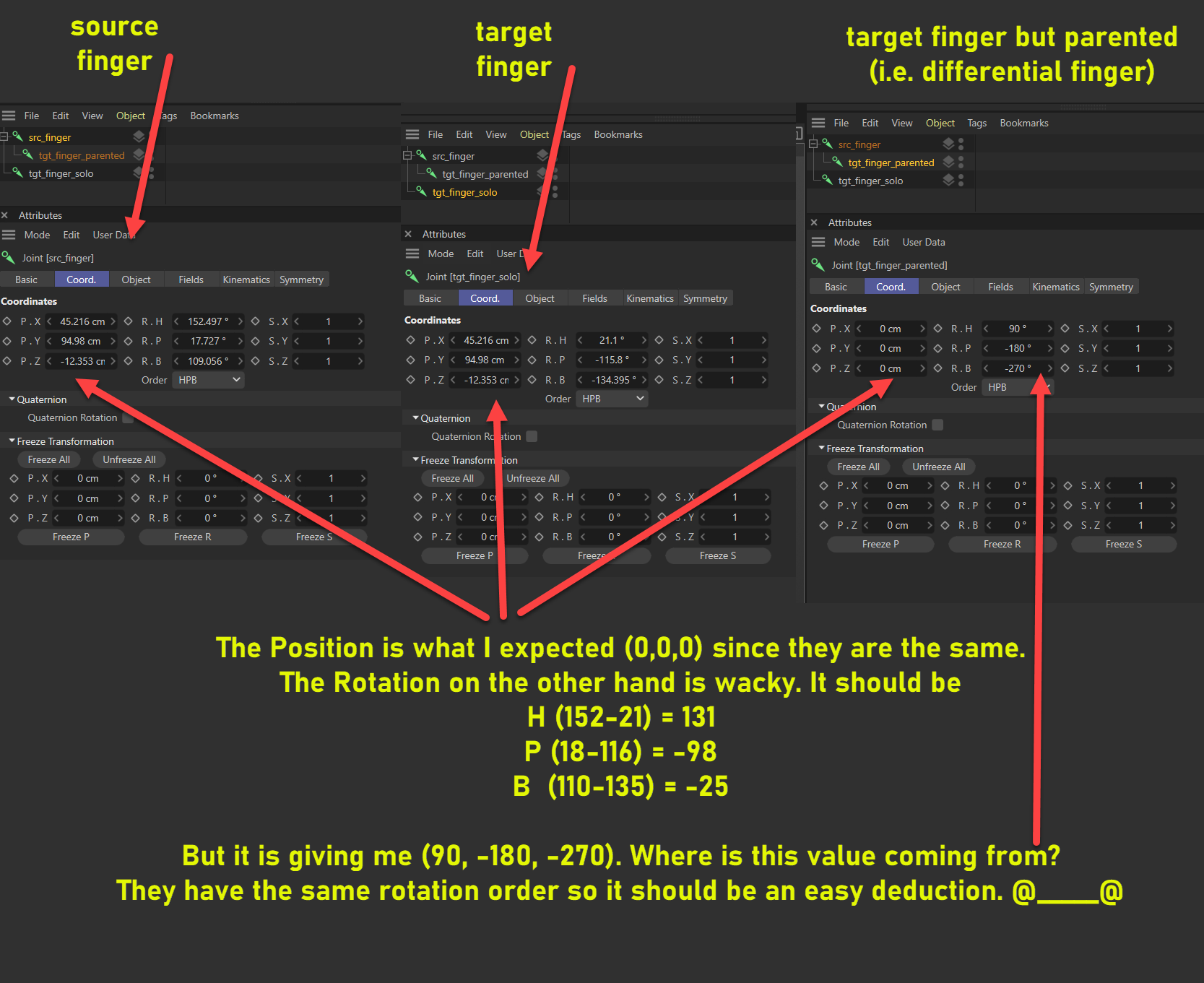
-
Another weird example
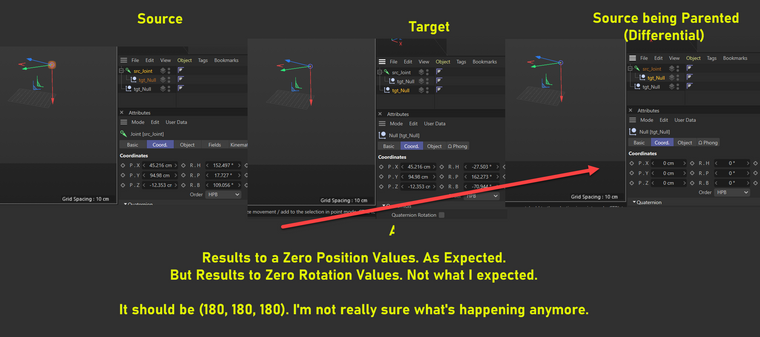
-
Hello @bentraje,
Thank you for reaching out to us. What you are trying to do there is simply not intended.
- As demonstrated in other threads of yours and by threads of other users, there is a tendency of users to gravitate towards (Euler) angles to express orientations programmatically. Probably because they are used to them from the app. This is a bad idea, if you want to deal with orientations programmatically, use matrices (a.k.a., frames or transforms) or other well accepted approaches such as quaternions. Angles are ambiguous and should be avoided.
- The Coordinate Manager is an artist tool, not a programming tool. It minimizes rotation distances and rounds values.
tgt_finger_parentedandtgt_finger_soloare not part of the same coordinate system (one is in the system ofsrc_fingerand one is in the world system), and therefore your computations fall flat.tgt_finger_soloandsrc_fingerare visually the same but not numerically due to floating point precision.
- We have the Matrix Manual which gives an introduction to the topic of expressing orientations as matrices.
I am not quite sure what the goal of this exercise is, but I assume you want to evaluate if two things have the same orientation. You must/should evaluate their global matrices then. Find an example below.
Cheers,
FerdinandThe result (I used your scene; I just renamed the objects to a, b, c):
a.GetName() = 'a' mgA = Matrix(v1: (0.157, -0.9, -0.406); v2: (-0.884, -0.311, 0.348); v3: (-0.44, 0.304, -0.845); off: (45.216, 94.98, -12.353)) b.GetName() = 'b' mgB = Matrix(v1: (-0.884, -0.311, 0.348); v2: (-0.44, 0.304, -0.845); v3: (0.157, -0.9, -0.406); off: (45.216, 94.98, -12.353)) c.GetName() = 'c' mgC = Matrix(v1: (-0.884, -0.311, 0.348); v2: (-0.44, 0.304, -0.845); v3: (0.157, -0.9, -0.406); off: (45.216, 94.98, -12.353)) mgB == mgC = False mgB.v1.x, mgB.v1.y, mgB.v1.z = (-0.8842901999875125, -0.31098271218515694, 0.3483110607179158) mgC.v1.x, mgC.v1.y, mgC.v1.z = (-0.8842901999875127, -0.3109827121851566, 0.3483110607179153) angleB = Vector(3.51, -1.121, 0.796), angleC = Vector(3.51, -1.121, 0.796) angleB == angleC = False angleB.x, angleB.y, angleB.z = (3.5098645832072863, -1.120505195429446, 0.7959503909437765) angleC.x, angleC.y, angleC.z = (3.5098645832072872, -1.1205051954294467, 0.7959503909437766) dotBC = 1.0 c4d.utils.CompareFloatTolerant(dotBC, 1.0) = True areAlinged(mgA, mgB) = False areAlinged(mgB, mgC) = TrueThe code:
import c4d doc: c4d.documents.BaseDocument # The active document def main() -> None: """ """ # Get the the three nodes in your document, I have renamed them to a, b, c. nodes: list[c4d.BaseObject] = doc.GetActiveObjects(c4d.GETACTIVEOBJECTFLAGS_CHILDREN) if len(nodes) < 3: return a, b, c = nodes[:3] # Get their global matrices and print them out. mgA: c4d.Matrix = a.GetMg() mgB: c4d.Matrix = b.GetMg() mgC: c4d.Matrix = c.GetMg() print (f"{a.GetName() = }\n{mgA = }\n") print (f"{b.GetName() = }\n{mgB = }\n") print (f"{c.GetName() = }\n{mgC = }\n") # a.GetName() = 'a' # mgA = Matrix(v1: (0.157, -0.9, -0.406); # v2: (-0.884, -0.311, 0.348); # v3: (-0.44, 0.304, -0.845); # off: (45.216, 94.98, -12.353)) # When two objects have the same orientation, the frames of their global matrices will be equal. # b.GetName() = 'b' # mgB = Matrix(v1: (-0.884, -0.311, 0.348); # v2: (-0.44, 0.304, -0.845); # v3: (0.157, -0.9, -0.406); # off: (45.216, 94.98, -12.353)) # c.GetName() = 'c' # mgC = Matrix(v1: (-0.884, -0.311, 0.348); # v2: (-0.44, 0.304, -0.845); # v3: (0.157, -0.9, -0.406); # off: (45.216, 94.98, -12.353)) # So, #b and #c seem to be "the same", right? print (f"{mgB == mgC = }\n") # mgB == mgC = False # The reason is floating point precision and the fact that the vector type is rounded in # print statements. When we compare the x/v1/i component of the mgB and mgC component-wise, # we can see that the vectors are very close but not the same. print (f"{mgB.v1.x, mgB.v1.y, mgB.v1.z = }") print (f"{mgC.v1.x, mgC.v1.y, mgC.v1.z = }\n") # mgB.v1.x, mgB.v1.y, mgB.v1.z = (-0.8842901999875125, -0.31098271218515694, 0.3483110607179158) # mgC.v1.x, mgC.v1.y, mgC.v1.z = (-0.8842901999875127, -0.3109827121851566, 0.3483110607179153) # We can convert these matrices to Euler angles and compare them, but this will have the same # problem. angleB: c4d.Vector = c4d.utils.MatrixToHPB(mgB) angleC: c4d.Vector = c4d.utils.MatrixToHPB(mgC) print (f"{angleB = }, {angleC = }") print (f"{angleB == angleC = }") print (f"{angleB.x, angleB.y, angleB.z = }") print (f"{angleC.x, angleC.y, angleC.z = }\n") # angleB = Vector(3.51, -1.121, 0.796), angleC = Vector(3.51, -1.121, 0.796) # angleB == angleC = False # angleB.x, angleB.y, angleB.z = (3.5098645832072863, -1.120505195429446, 0.7959503909437765) # angleC.x, angleC.y, angleC.z = (3.5098645832072872, -1.1205051954294467, 0.7959503909437766) # So, the solution is simple, as always with floating point values, we should not test for # being identical but for being very close. The easiest way to do this with vectors is the dot # product, i.e., measure their spanned angle. We can use CompareFloatTolerant for that, although # I am personally not a big fan of this function, as it takes control away from you. # Calculate the dot product of the normalized #b and #c vectors (so that their length does not # contribute). When ~b and ~c are the same vector, their product should be 1.0. As the # dot product for parallel unit-vectors is 1, for anti-parallel unit-vectors -1, and for # orthogonal unit-vectors 0. In practice, we might have to compensate for floating point # precsion with an error tolerance epsilon. dotBC: float = ~angleB * ~angleC print (f"{dotBC = }") print (f"{c4d.utils.CompareFloatTolerant(dotBC, 1.0) = }\n") # dotBC = 1.0 # c4d.utils.CompareFloatTolerant(dotBC, 1.0) = True # I personally would not do it like this, I would compare the frames (i.e., the three vectors in # a matrix/transform that express orientation and scale) directly. def areParallel( a: c4d.Vector, b: c4d.Vector, directional: bool = True, epsilon: float = 1E-6 ) -> bool: """Tests if #a and #b are parallel within the tolerance #epsilon. Args: a, b: The vectors to compare. directional: If True, only truly parallel vectors (th ~= 0) will be considered parallel. if False, also anti-parallel vectors will be considered parallel (th ~= 180). Defaults to True. epsilon: The decimal precision for the comparison. Defaults to six places. """ theta: float = ~a * ~b if directional else abs(~a * ~b) return abs(theta - 1.0) <= epsilon def areAlinged(a: c4d.Matrix, b: c4d.Matrix, epsilon: float = 1E-6) -> bool: """Tests if #a and b# have the same orientation within the tolerance #epsilon. Args: a, b: The matrices to compare the orientation for. epsilon: The decimal precision for the comparison. Defaults to six places. """ return (areParallel(a.v1, b.v1, epsilon=epsilon) and areParallel(a.v2, b.v2, epsilon=epsilon) and areParallel(a.v3, b.v3, epsilon=epsilon)) print (f"{areAlinged(mgA, mgB) = }") print (f"{areAlinged(mgB, mgC) = }") # areAlinged(mgA, mgB) = False # areAlinged(mgB, mgC) = True if __name__ == '__main__': main() -
Gotcha. Thanks for the clarification and the sample code. Should have probably went for the matrix transforms to begin with. I was hoping I can get away with those euler angles lol.
Closing the thread now.