Retrieving Viewport Camera Matrix
-
Hello,
I'm trying to get the matrix from the active camera view in a scene, I can get the matrix from a camera in the scene fairly easily and from the viewport in perspective mode.
I'm running into trouble when getting the matrix from the viewport camera when it is one of the other modes: top, right, front, etc.
I tried using the code from the BaseView/BaseDraw Manual to get the matrix.
BaseDraw* const baseDraw = doc->GetActiveBaseDraw(); if (baseDraw == nullptr) return maxon::IllegalArgumentError(MAXON_SOURCE_LOCATION); BaseObject* const cameraObject = baseDraw->GetEditorCamera(); // move active object into the camera view const Matrix cameraMatrix = cameraObject->GetMg();It works properly when the camera is in "Perspective" mode, in every other mode the angle from the matrix is not the right result. Is there another way that I should be doing this?
Any help would be greatly appreciated.
John Thomas
-
According to the documentation, the midpoint of orthogonal projections is set with the "Offset" property.
See CameraObject Manual.
-
Hi @JohnThomas thanks for reaching out us. According to @PluginStudent remark you can use the
CameraObject::GetOffset()to place the object at the center of the active orthogonal view, but if you also need to orient the object according to the view you should also consider to use theBaseView::GetMg()which orient and locate the active object.Best, R
-
Thanks for the responses.
I am able to use BaseDraw::GetMg() to get the proper orientation from the active view for most of the different modes. When I try using that method on the Military, Gentleman, Bird, and Frog modes it is returning an orientation vector that is clearly not right.
Is there a different method needed to retrieve the data from those camera modes?
John Thomas
-
Hi @JohnThomas,
I've tried all the cases and I can't spot anything with the above solution.
Assuming you create a 3 sides pyramid pointing to -Z by default, you have:
- Top:
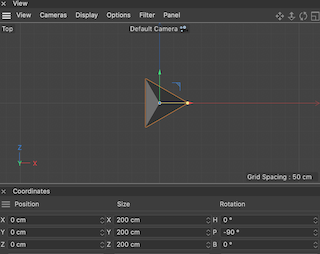
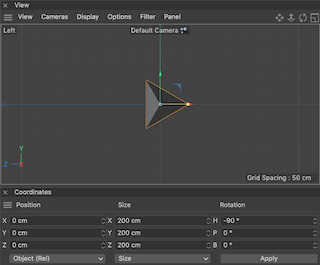
- Left:
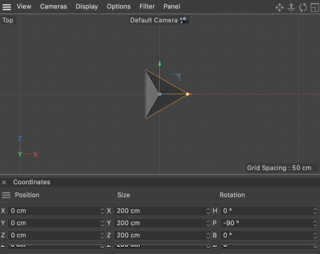
- Front:
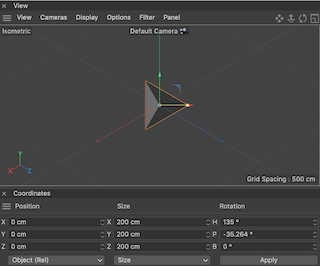
- Isometric:
- Dimetric:
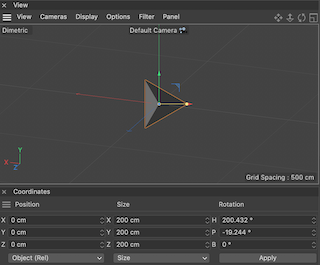
With regard to orthogonal axonometries, given that the result of an axonometric procedure is a uniformly-scaled parallel projection of the object and considering the following drawing conventions (right-hand coordinate) where cavalier == gentlemen we still have correct representations.
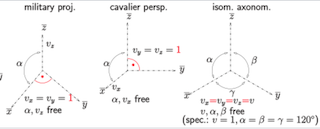
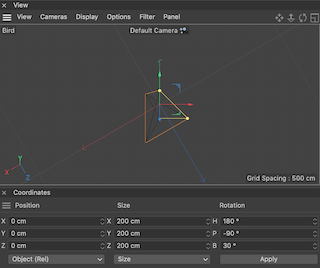
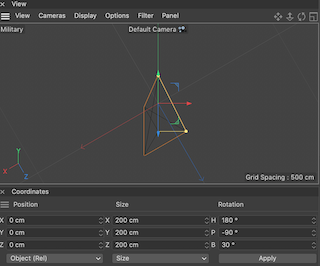
Given the above convention, in a left-hand coordinate system, for Bird, Military and Frog (which are ortographic axonometries) the results is correct because the base of the pyramid still look correct and oriented properly (with the Y axis being represented with different scale)
- Bird:
- Military:
- Frog:
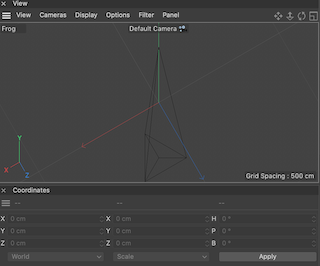
as well as - Gentlemen:
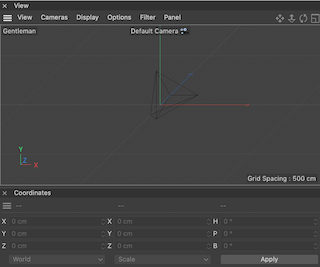
- Top:
-
Hi,
I might be misunderstanding the spirit of the question, but I think you misunderstood the question (and misconecption) of @JohnThomas. The bottom line is - the fixed orthographic projections "do not point", or slightly less naive - the transform of a camera object does not (necessarily) reflect a camera projection transform in these cases. You have to "emulate" these on your own. Here is some Python code which should illustrate the problem.
"""Run this in the script manager and read the commented code. It should clear up some misconceptions. """ import c4d def main(): """ """ # Create a new camera and set its offset to a distinctive value. camera = c4d.BaseList2D(c4d.Ocamera) if camera is None: raise MemoryError() doc.InsertObject(camera) camera.SetMg(c4d.Matrix(off=c4d.Vector(100))) # Go over the projection modes of our camera object. msg = "projection: {}\nframe:\n\t{}\n\t{}\n\t{}\noffset: {}\n" for pid in range(14): camera[c4d.CAMERA_PROJECTION] = pid c4d.EventAdd() # Judging by your code, you do expect this transform to change, # depending on the projection mode, i.e. be some kind of camera # projection transform. But it is not, it is just the same old # transform of the camera object. mg = camera.GetMg() # What the C++ Doc's sell you as the midpoint/offset of the camera # is just the offset of the transform of the camera object. if mg.off != camera.GetOffset(): raise ValueError("This should not happen.") # Print out the data. print msg.format(pid, mg.v1, mg.v2, mg.v3, mg.off) # Bottom line - you cannot access the camera projection transforms # in Cinema and have to recreate them more or less faithfully on your # own. # Or in other words, changing the projection mode of the camera # does not change where it "points". if __name__ == "__main__": main()Cheers,
zipit -
Hi @zipit, thanks for joining the thread, you insights are always very appreciated.
Your example shows, as expected, that the camera transformation matrix doesn't change when switching between different projection modes, because Cinema 4D decouples camera transformation from BaseView transformation and, I think, I never said that the camera changes its orientation when switching among projections.
The point is to understand what is the final goal of @JohnThomas because arguing from his initial code seems like he wants to move an object into the camera view which can be just by moving the object into the camera center or by also re-orienting the object in the current projection space.
I just had to explain where the correct matrix orientation should be found (BaseView::GetMg()) and to show that the matrix values are correct respect to the different projections.
Cheers, R
-
Hi,
wasn't arguing that this is your misconception @r_gigante, but @JohnThomas's. He shows getting the global transform of a camera object and then talks about an "orientation vector clearly not being right".
This is phrasing of his is a bit ambiguous, which is why I said I might be misunderstanding something here, but I red it as if he was expecting the projection plane of the camera to always be aligned with the xy plane of the transform of the camera object. So I just pointed out that this is not guaranteed in all projection modes.
Cheers,
zipit -
Thanks for the detailed response @r_gigante, sorry about the late post. I wasn't trying to move an object into the camera view, I was just trying to get the information about a cameras perspective so that if necessary I could create an object that would have an orientation parallel to it.
John Thomas